1.2 二进制加法器和减法器

在本教程中，我们将研究二进制加法器和减法器电路。我们将学习半加器、全加器、并行加法器（使用多个全加器）、半减器、全减器以及并行加法器/减法器组合电路。

二进制加法电路

加法和减法是任何数字计算机必须执行的两种基本算术运算。如果这两种运算能够正确实现，那么乘法和除法任务就会变得简单（因为乘法是重复加法，而除法是重复减法）。

考虑将两个二进制数相加的操作，这是数字计算机执行的一项基本任务。两个单比特二进制数的四种基本加法运算如下：

• $0 + 0 = 0$
• $1 + 0 = 1$
• $0 + 1 = 1$
• $1 + 1 = (\text{进位})1\ 0$

在前三种运算中，每次二进制加法的结果是一个比特，即0或1。但对于第四种加法运算（输入为1和1时），结果由两个二进制位组成。在这里，低位称为“和位”，而高位称为“进位位”。

对于单比特加法，可能没有问题。但是，当我们尝试对多位二进制数进行加法运算时，可能会出现问题。

设计用于对两个二进制数进行加法运算的逻辑电路称为二进制加法器电路。根据它们如何处理“1+1”加法的输出，它们被分为：

• 半加器
• 全加器

让我们来看一下各种加法器电路执行的二进制加法。

半加器

用于对两个1比特数或简单地说两个比特进行加法运算的逻辑电路称为半加器电路。该电路有两个输入和两个输出。输入是两个1比特二进制数（称为被加数和加数），输出是和与进位。

下图展示了半加器的框图。

半加器的真值表如下表所示。

INPUT	OUTPUT
A	B
0	0
0	1
1	0
1	1

如果我们观察上述真值表中的“和”值，它类似于异或门（XOR）。同样，上述真值表中的“进位”值类似于与门（AND）。

因此，为了正确实现半加器，你需要两个逻辑门：一个异或门用于“和”输出，一个与门用于“进位”输出。下图展示了半加器的逻辑图。

在上述半加器电路中，输入标记为 A 和 B。“和”输出标记为求和符号（∑），进位输出标记为 CO。

半加器主要用于对第一阶二进制数（即1比特二进制数）的被加数和加数进行加法运算。我们不能对超过1比特的二进制数进行加法运算，因为半加器无法包含来自前一次加法的“进位”信息。

由于这种限制，半加器在许多应用中实际上并未被广泛使用，尤其是在多位数加法中。在这些应用中，前一位加法的进位必须与两个比特一起相加，因此它是一个三比特加法。

全加器

全加器是一种组合逻辑电路，它对三个比特进行加法运算，并产生两个输出：一个和与一个进位。正如我们所见，半加器无法响应三个输入，因此全加器用于一次加三个数字。

它包含三个输入，其中两个是输入变量，表示要相加的两个有效比特，而第三个输入端是来自前一次加法的进位。两个输出是和与进位输出。

下图展示了全加器的框图，输入标记为 A、B 和 CIN，而输出标记为 ∑ 和 COUT。

全加器的真值表如下表所示。

INPUT			OUTPUT
A	B	CIN	Sum	COUT
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

从上述真值表中，我们可以获得和与进位输出的布尔表达式。使用这些表达式，我们可以构建全加器的逻辑电路。但通过进一步简化方程，我们可以得出全加器可以很容易地使用两个半加器和一个或门来实现。

下图展示了使用两个半加器和一个或门实现的全加器电路。在这里，A 和 B 是主要输入比特，CIN 是进位输入，∑ 和 COUT 分别是和与进位输出。

并行二进制加法器

正如我们所讨论的，单个全加器执行两个1比特数的加法以及进位输入。对于执行超过1比特的二进制数的加法，需要多个全加器，全加器的数量取决于比特数。因此，并行加法器是由多个全加器组成的，用于同时对两个数的所有比特进行加法运算。

通过将 $n$ 个全加器并联连接，可以构建一个 $n$ 位并行加法器。从下图可以看出，最低有效位处没有进位，因此我们可以在这里使用半加器，或者将全加器的进位输入设置为零。

下图展示了一个4位并行二进制加法器，它包含三个全加器和一个半加器。要相加的两个二进制数是 $A_3 A_2 A_1 A_0$ 和 $B_3 B_2 B_1 B_0$，它们被应用到全加器的相应输入端。这个并行加法器产生它们的结果为 $C_4 S_3 S_2 S_1 S_0$，其中 $C_4$ 是最终进位。

在4位加法器中，第一个模块是一个半加器，其输入为 $A_0 B_0$，产生和 $S_0$ 和进位比特 $C_1$。第一个模块也可以是全加器，如果是这样，那么输入进位 $C_0$ 必须为0。

接下来的三个模块应该是全加器，因为它们有三个输入（两个主要的二进制比特和来自前一阶段的进位比特）。

因此，第二个模块的全加器产生和 $S_1$ 和进位 $C_2$。这将依次被其他两个全加器跟随，因此最终结果是 $C_4 S_3 S_2 S_1 S_0$。

通常，全加器是设计在双列直插式封装集成电路中的。74LS283 是一种流行的4位全加器集成电路。计算机的算术逻辑单元（ALU）包含这些并行加法器，用于执行二进制数的加法。

二进制减法电路

数字计算机需要执行的另一种基本算术运算是减法。减法是一种数学运算，其中一个整数从另一个整数中减去以获得等效的量。被减去的数称为“被减数”，从被减数中减去的数称为“减数”。

与二进制加法类似，二进制减法也有四种可能的基本运算。它们是：

• $0 - 0 = 0$
• $0 - 1 = (\text{借位})1\ 1$
• $1 - 0 = 1$
• $1 - 1 = 0$

上图展示了二进制减法的四种可能规则或基本运算。在所有运算中，每个减数位都从被减数位中减去。

但在第二条规则中，被减数位小于减数位，因此需要借1来进行减法运算。与加法器电路类似，基本减法器电路也有两种类型：

• 半减器
• 全减器

半减器

半减器是一种具有多个输出的组合逻辑电路，用于对两个1比特二进制数进行减法运算。它有两个输入和两个输出。两个输入分别对应于两个1比特二进制数，而两个输出分别对应于差值位和借位（与半加器中的和与进位相反）。

半减器的真值表如下表所示。

INPUT		OUTPUT
A	B	Difference	Borrow
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

从上述真值表可以看出，半减器的“差值”输出类似于异或门（XOR）的输出（这也与半加器的和输出相同）。因此，半减法运算也可以通过异或门和一个与门来实现，其中与门的一个输入取反，另一个输入保持正常，以实现借位运算。

下图展示了半减器的逻辑电路。

该电路与半加器类似，唯一的区别在于被减数输入 A 在应用于与门之前被取反，以实现借位输出。

在多位数减法的情况下，两个数字之间的减法必须与前一位数字减法的借位一起进行，因此减法器需要有三个输入，这在半减器中是不可能的。因此，半减器的应用范围有限，严格来说，在实际中并不被使用。

全减器

全减器是一种组合逻辑电路，用于对两个1比特二进制数进行减法运算，并且它还考虑了前一位的借位，即前一位被减数是否借了1。

因此，全减器有三个输入，其中两个输入对应于要相减的两个比特（被减数 A 和减数 B），还有一个借位比特，通常表示为 BIN，对应于借位操作。有两个输出，一个对应于差值 D 输出，另一个是借位输出 BO。

下图展示了全减器的框图。

全减器的真值表如下表所示。

INPUT			OUTPUT
A	B	BIN	D	BOUT
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

通过从上述真值表中推导出全减器的布尔表达式，我们得到一个表达式，表明全减器可以用半减器和或门实现，如下图所示。

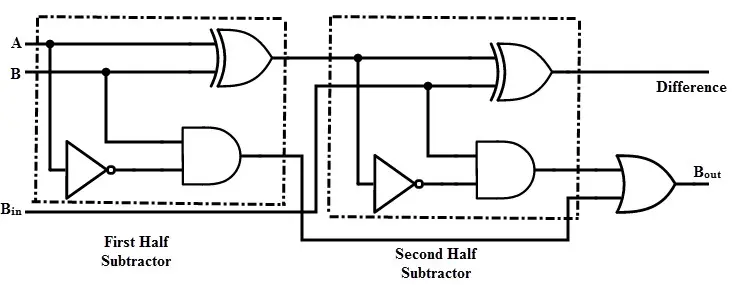
通过比较加法器和减法器的电路和真值表，我们可以观察到全减器中的输出 D 与全加器中的输出 S 完全相同。唯一的区别是全减器中的输入变量 A 被取反。

因此，可以通过在将输入 A 应用于门电路之前对其进行取反，将全加器电路转换为全减器，以产生最终的借位输出 Bo。

并行二进制减法器

为了执行多位二进制数的减法，我们需要使用并行减法器。这种并行减法器可以通过多种方式设计，包括半减器和全减器的组合、全部使用全减器、全部使用全加器并输入减数的补码等。

下图展示了一个4位并行二进制减法器，它由一个半减器和三个全减器连接而成。

在这个减法器中，4位被减数 $A_3 A_2 A_1 A_0$ 减去4位减数 $B_3 B_2 B_1 B_0$，结果是差值输出 $D_3 D_2 D_1 D_0$。每个减法器的借位输出连接到下一个减法器的借位输入。

也可以使用4个全加器设计一个4位并行减法器，如下图所示。该电路通过考虑被减数与减数补码相加等同于减法过程的原则来执行减法运算。

我们知道，A 减去 B 的结果可以通过取 B 的2的补码并将其加到 A 上来获得。B 的2的补码是通过对 B 取1的补码并在最低有效位对上加1得到的。

因此，在这个电路中，B 的1的补码通过反相器（NOT 门）获得，并且可以通过输入进位将1加到和上。

并行加法器/减法器

加法和减法的运算可以通过一个通用的二进制加法器来完成。这种二进制电路可以通过在每个全加器上添加一个异或门来设计，如下图所示。下图展示了一个4位并行二进制加法器/减法器，它有两个4位输入：$A_3 A_2 A_1 A_0$ 和 $B_3 B_2 B_1 B_0$。

模式输入控制线 M 连接到全加器最低有效位的进位输入。这条控制线决定了执行的操作类型，是加法还是减法。

当 M = 1 时，电路为减法器；当 M = 0 时，电路变为加法器。异或门有两个输入，其中一个连接到 B，另一个连接到输入 M。当 M = 0 时，B 与 0 进行异或运算，结果为 B。然后，全加器将 B 与 A 相加，进位输入为零，因此执行加法运算。

当 M = 1 时，B 与 0 进行异或运算，结果为 B 的补码，并且进位输入为 1。因此，补码后的 B 输入与 A 相加，并通过输入进位加上 1，这实际上是一个2的补码操作。因此，执行了减法运算。